Cebirsel ifadelerde modelleme kavram yanilgilari

 

Görsel Matematus yayınları 7.sınıf Matematik Alıştırma ve soru Bankası kitabından alınmıştır .


Görsel Zeka Küpü Yayınları 7.sınıf matematik soru bankası kitabından alınmıştır .

iki örneğe dikkatinizi çekmek çekmek istiyorum , +x ve +1 lerin modellenmesinde herhangi bir sorun gözükmüyor , ancak -x ve -1 in modellenmesi sıkıntılı , çünkü uzaklık mutlak değer bir olgudur ve - ile gösterilemez . Uzaklık için en fazla 0 diyebilirsiniz. Örneğin Ankara ile istanbul arasını -600 km diyemezsiniz , Ya da şekille gösteremezsiniz.
Yukarıda verdiğim iki örnekte ve piyasada bulunan hemen hemen tüm matematik kaynak kitaplarında ( meb in verdiği kitaplarda var mı bilmiyorum ) bu kavram yanılgısıyla karşılaşıyorum .

\( \displaystyle 3(x-1)\) ve  \( \displaystyle 2(3x-2)\) ifadelerini  nasıl modellemiş bakalım ;

 

Gri bölgeler + ları , ( +x ve +1 ) turuncu bölgeler için - leri ( -x ve -1 ) temsil ediyor demiş yukarıda ;

ilk örnekte dikey \( \displaystyle x-1 \)  i , yatay ise 3 .

ikinci örnekte dikey +2 yi , yatay \( \displaystyle 3x-2 \) yi temsil etmiş ,

Örnekler sanki + ların yanına - bölgeler eklenmiş gibi ..- bölge olması matematiksel olarak hatalı olduğu gibi , eklenmesi de hatalı . Karenin bir kenar uzunluğunun -1 br olması imkansızdır .

Doğru modelleme nasıl olmalıydı ?

 

x br uzunluktan 1 br uzunluk çıkarılarak x-1 birim uzunluk elde edildi .

 

\( \displaystyle x \)  kadar birim uzunluktan 1 birim uzunluk çıkarılmalıydı , \( \displaystyle 3(x-1) \) kalan alan ; 3x birim alandan 3 birim alanın çıkarılmasıdır .

2. Örneğin doğru modellemesi şu şekilde olmalıydı .  \( \displaystyle 2(3x-2) \) ;


3x br uzunluktan 2 birim uzunluk çıkarılarak 3x-2 br uzunluk elde edildi .

Kalan alan ki bu \( \displaystyle 2(3x-2) \)  demek , \( \displaystyle 6x \) br alandan , 4 br alanın keserek çıkarılmasına denktir .

 

Tüm bunlar , çarpmanın alan anlamının öğrencilere öğretilmemesinden kaynaklanıyor , örneğin verilen şekle neden x dendiğini öğretilmeden yüzeysel olarak şekiller bunlar , modelleme de bu bakış açısından kaynaklanıyor .

Bu şekillere neden x , 1 ve x² diyoruz ? 



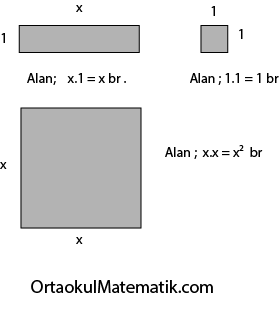
Yorumlar

Yorum Gönder

Bu blogdaki popüler yayınlar

Tam sayılarda bölme

 Tam sayılarda bölme işleminde , ortaokul için bölmeyi yapıp işareti koymak kalıyor , nasıl bölme yapılacağı ilkokul konusudur . Örneğin 72 yi 12 ye nasıl böleceğinizi ilkokulda öğrenmeniz gerekiyor .Bunu yapamıyorsanız ,  hesap makinası kullanın ! Ortaokulda bilmeniz gereken   işaretlerin durumudur . + : + =  +  Artının artıya bölümü artı - : - = +   Eksinin eksiye bölümü ARTI - : + = -  Eksinin artıya bölümü eksi + : - = - Artının eksiye bölümü - Aynı işaretlerin birbirine bölümü + , farklı işaretlerin birbirine bölümü - dir . 12: 2 = 6   Her iki sayı da pozitif sonuç pozitif -30 : (-2 ) = 15  Her iki sayı da pozitif sonuç pozitif . 30 : (-2 ) = -15  sayıların işaretleri farklı sonuç negatif -30:2 =-15  sayıların işaretleri farklı sonuç negatif Peki , neden -2 yi parantez içine aldım da , -30 u almadım ?   Aladabilirdik , almamız -30 için sorun çıkartmaz ama , -2 yi almamamız sorun çıkartır , matematikte iki işaret yan yana ...
Devamı

Sözel ifadeleri cebirsel olarak yazma

Sözel olarak verilen ifadeleri cebirsel olarak  nasıl yazabiliriz bakalım ; Herhangi bir sayı : \(x\) Bir sayının 5 fazlası : \(x+5\) Bir sayının 3 eksiği : \(x-3\) Bir sayının 3 e bölümü : \(\large\frac{x}{3} \) Bir sayıyla 10 un toplamı : \(x+10\) Bir sayının -2 eksiği  \(x-(-2)\) 30 liradan bir miktar para harcarsam , geriye kalan : \(30-x\) Bir sayının 7 katı : \(7.x\) yani \(7x\) Bir sayının 7 katının 5 fazlası : \(7x+5\) Bir sayının 5 fazlasının 7 katı : \((x+5).7\) Bir sayının yarısının 9 eksiği : \(\large\frac{x}{2} - 9 \) Bir sayının 9 eksiğinin yarısı :\(\large\frac{x-2}{9}  \) Bir sayının \(\large\frac{3}{5}  \) ü ; \(x.\large\frac{3}{5} = \large\frac{3x}{5}\) Bir sayının karesi : \(\large x²\) Bir sayının küpü : \(x³\)  
Devamı

Nokta, Doğru , Doğru Parçası , Işın

Resim
  Nokta ; Düzlemde yüzeyde bulunan kesin yer / konumdur . Noktanın  fiziksel birşey olmadığını anlamak önemlidir, Noktanın  yerini belirtmek için kalemle bir "pıtt" ( nokta ) koyarız. Örneğin bu noktanın çapı 0.2 mm olabilir  , ama boyutunun olmadığı kabul edilir. Çünkü ; Nokta , soyut bir kavramdır . Bir "konum" dur. Boyutu yoktur.  Noktalar büyük harflerle gösterilirler   Doğru : Her iki yönden sonsuza kadar giden aynı doğrultudaki noktalar kümesi .  Tek boyutludur , sadece uzunluğu vardır , genişliği yoktur . Doğrunun uzunluğu ölçülemez. Sizin çizdiğiniz tüm doğrular , gerçek doğru değildir . Siz doğru modeli çiziyorsunuz .   Gerçek doğru çizilemez , çünkü sonsuza kadar gitmemiz gerekir ..Gerçek dünyada doğru diye bişey yoktur , tüm gördükleriniz doğru parçası modelleridir. ipince bir ip düşünün ve bu ipin sonsuzdan gelip sonsuza kadar gittiğini .. Doğru parçası  Adı üzerinde , doğrudan bir parçadır . Doğrunun bir bölümü..   Doğru pa...
Devamı