Paralelkenarın alanı
Şekillerin alanlarını karelerle ölçeriz , dolayısıyla paralelkenarın alanını da karelerle ölçer ve kare cinsinden ifade ederiz.
Paralelkenarın alanı demek , paralelkenarın içine ne kadar / kaç tane birim karelerden sığdırabilirim demektir.
Eğer şeklimiz paralelkenar değil de , kare ya da dikdörtgen olsaydı ölçmem / hesaplamam çok basit olurdu . Hem şekil olarak basit olurdu , hem de karenin ve dikdörtgenin alanını hesaplamasını daha önce öğrendiniz.
Tabanda 12 kare var ve , toplam 7 sıra .. 12*7= 84 birim kareden oluşmakta .
Peki aşağıda verilen paralelkenar kaç kareden oluşmakta ?
Tam olan kareleri rahatlıkla sayabiliriz ancak , tam olmayan kareler problem gibi gözüküyor . Bu sorunu aşmak için çözümler aramalıyız.
Temel yaklaşım : Bilmediğimiz şekilleri , bildiğimiz şekillere çevirebilirsek daha basit şekilde hesaplama yapabiliriz .
O halde paralelkenarı , dikdörtgene , kare ya da üçgene çevirmeli ya da bunlardan yararlanarak alanını hesaplamalıyız.
Yaklaşım 1 : Paralelkenarı dikdörtgene çevirmeye çalışalım .
Paralelkenarın kulağından kesip diğer tarafa yapıştıralım .
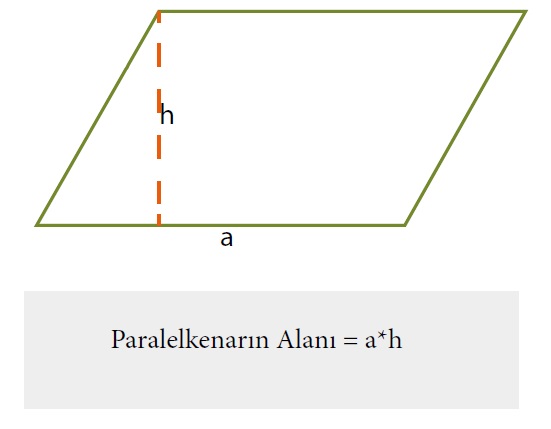
Paralelkenarın alanı Taban ve tabana ait yüksekliğin çarpımına eşittir.
Yüksekliği “h” harfiyle göstermemizin nedeni ingilizce yükseklik anlamına gelen “height” kelimesinden gelmektedir.
Yaklaşım 2: Paralelkenarın alanını üçgen yardımıyla bulalım
Paralelkenarı köşelerden iki üçgene ayıralım.
Taralı olan üçgenin alanı :
$$\frac{a.h}{2}$$
Taralı olmayan üçgenin alanı :
$$\frac{a.h}{2}$$
Üçgenlerin toplam alanı = Paralelkenarın Alanı
$$\frac{a.h}{2}+\frac{a.h}{2}=\frac{2.a.h}{2}=a.h$$
Gördüğünüz gibi aynı sonucu elde ettik .
Paralelkenarda taban ve yüksekliği her zaman alıştığımız şekilde olmak zorunda değildir . Sağ ya da sol kenarlardan biri de taban olabilir .
Bu durumda da , paralelkenarın alanı için taban * tabana ait yükseklik formülü geçerlidir.
Paralelkenarı iki üçgene ayırabiliriz ;
Taralı olan üçgenin alanı :
$$\frac{a.h}{2}$$
Taralı olmayan üçgenin alanı :
$$\frac{a.h}{2}$$
Üçgenlerin toplam alanı = Paralelkenarın Alanı
$$\frac{a.h}{2}+\frac{a.h}{2}=\frac{2.a.h}{2}=a.h$$
Bu anlatımı bilgisayarına Pdf formatında indirebilirsin













Yorumlar
Yorum Gönder